Space-efficient Resizable Arrays
19/Dec 2012
This post is about resizable arrays that would serve as an alternative to std::vector. You’re probably familiar with geometrically growing arrays like std::vector, so I won’t waste time describing them in detail. Briefly, they offer amortized constant-time append and lookups, but with a pretty severe cost to space overhead (as low as 33% utilization, after shrinking until you hit a realloc, or 50% if all you ever do is append). Another issue is that the elements of the array get copied ever so often. The exact number of times an element gets copies depends on the initial size and total size of the vector, but roughly speaking expect north of 2 extra copies per element, in addition to any copy you had to do to get the data into the vector in the first place. This can be very expensive for big objects, and perhaps more importantly isn’t very consistent – occasionally you get a big hiccup as every single element is copied.
The data structure I’m describing has constant-time random access, append, etc. like std::vector, but at a fraction of the storage overhead, and with no extra copies of the elements. There are occasional spikes, but they amount to a single allocation (or deallocation) – no copying. The tradeoff is a more complicated procedure for random access (still efficient, and constant time, but certainly much more complicated than just a simple pointer addition like std::vector can do).
I ran into the paper “Resizable Arrays in Optimal Space and Time” a couple of weeks ago, and thought all this sounded pretty great. Especially for modern architectures where ALU work is cheap, relatively speaking. The basic idea is to represent arrays as an array of pointers to data blocks. This first array is called the “index block”. The data blocks get bigger and bigger as the total amount of elements increases. They’re roughly O(√n)-sized. This is enough that the size of the index block itself quickly becomes irrelevant because the data blocks dwarf the cost of tracking it in the index block. For all this to be practical, we need there to be an efficient, constant-time, method to discover which data block a given “virtual index” resides in. Then we can fetch from that data block using the index block as an indirection.
The paper describes the basic structure of this, as well as some motivation and proof of its asymptotic properties, so I won’t repeat it here. The key point is that each block is roughly √n-sized (with n being the size of the array at the time that block was allocated – early blocks are small, and later blocks are large). Only the last block is non-full, so the total amount of space overhead at any one time is O(√n). Because we only ever add (or remove) blocks, never reallocate them, we don’t need to copy any elements. This non-moving property also makes this data structure suitable for memory pools and such (growing the array won’t cause existing elements to move around - which is the usual problem with using std::vector for pools).
Looking around on the web, though, I couldn’t find anyone who had actually implemented this. This seemed curious and slightly worrying to me. I decided to implement a basic version in C++ whenever I had time. Well, after attempting an implementation I discovered that the paper has a critical bug in the core algorithm. I also found that others had indeed attempted to implement this and run into the same issue (see for example this email exchange). Turns out that the computation of p in the Locate algorithm is just plain incorrect (likely a typo – it corresponds to computing the number of data blocks for a single super block, rather than the total sum of data blocks for all super blocks up until that super block index).
Anyway, after much hassle I was able to arrive at a corrected version of this algorithm. Wordpress won’t let me paste code in here (even when editing the markup manually with the code tag), so I’ll just refer you to the locate_data_block_and_elem method. While I used some MSVC intrinsics to do a couple of the bit-fiddling operations a bit more efficiently, I haven’t spent any major energy optimizing it (this is the place to optimize though, I’d say). Feel free to improve on this in the comments J!
Here’s a link to the implementation: compact_vector. Note, this is very basic, and probably has bugs. It does the main things, but there’s plenty of stuff you’d need to add to make this industrial strength (e.g. right now I rely on elements having a default constructor, have no support for custom allocators etc.). It basically follows the main ideas of the paper, except that instead of tracking the size of the current block and super block (doubling each alternately), I just compute these two values from the number of super blocks each time they’re needed (this turned out to be no slower, and reduced the number of book-keeping variables, as well as simplified the code). I also keep the “spare” empty data block in a separate pointer instead of storing it in the index block, to keep the code a bit cleaner (no need to keep checking for this special case – the index block only refers to data blocks in actual use).
So here are some quick benchmarks. This is on one machine, without any real attempt to be super-rigorous, etc. etc., your mileage may vary, yadda, yadda. All benchmarks are for 50k elements. First, let’s look at appending 4 byte integers.
| **Array type ** | **Cycles per element** |
| Compact vector append time (4 bytes) | 35.8 |
| std::vector append time (4 bytes) | 45.0 |
So we’re already 20% faster than std::vector for insertions. Likely because we don’t have to do all those extra copies. By the way, the space overhead for the compact vector here is about 2%.
Using some fatter elements, say 16 bytes, the difference is even more pronounced:
| **Array type ** | **Cycles per element** |
| Compact vector append time (16 bytes) | 152.2 |
| std::vector append time (16 bytes) | 283.6 |
That’s about 46% faster. Okay, so now that we have the good news out of the way, what’s price we pay for this? I mean look at that function mentioned above, clearly we’re paying some cost to index into this thing, right? Well, yes of course, there’s no free lunch. For random access we see the following picture:
| **Array type ** | **Cycles per element** | **Ratio to std::vector** |
| Compact vector random access (4 bytes) | 16.6 | 8.3 |
| std::vector random access (4 bytes) | 2.0 | |
| Compact vector random access (16 bytes) | 18.1 | 7.9 |
| std::vector random access (16 bytes) | 2.3 | |
| Compact vector random access (64 bytes) | 20.6 | 4.0 |
| std::vector random access (64 bytes) | 5.1 |
This is for a loop that just goes straight through the array of integers and sums up the elements, using random access reads. This access pattern should be a worst case scenario for compact array relative the much simpler std::vector since it reduces the impact of cache misses (and indeed the relative cost difference goes down as the element size goes up).
However, rather than just focus on that massive 8x ratio number, I think it may be more interesting to look at the absolute values of the timings here. We’re talking about 17 cycles per element, including the loop overhead and the actual addition itself. In many cases where you do random access reads on std::vectors you end up doing far more work than that per element – especially if the accesses are truly random so you incur a cache hit per access (although technically for the compact array you may end up with two cache misses, the index block is small so you’re a lot more likely to get a hit there than on the full array).
For coherent reads, i.e. using iterators, we can do much better. We don’t need to translate the virtual index to a data block and intra-block index for each element, we can just step through the data blocks directly instead. We still need to do a check for each element to make sure we’re still in the same data block, and some minor computation to advance from one data block to the next (relating to computing the next block’s size), but the fast path is a quick pointer increment and compare which saves a lot of overhead:
| **Array type ** | **Cycles per element** |
| Compact array iterator scan time (4 bytes) | 6.9 |
| std::vector iterator scan time (4 bytes) | 1.51 |
Here’s a graph of total storage used over time:

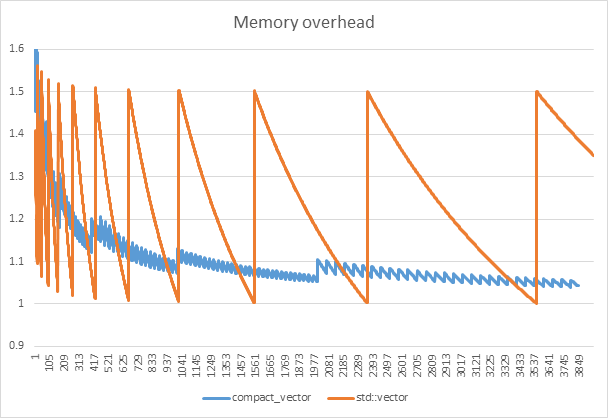
This is fairly typical behavior. The standard std::vector gets very good efficiency when the number of elements happens to be close, but below the current size of the underlying array, but you’re oscillating between 50% and close to 0%, averaging out at 25% overhead. In contrast, compact_vector has a bit more fixed overhead and some extra overhead for the the index block, but the storage requirements grows relatively smoothly (you can’t see it in the graph, but it does oscillate, just not quite as wildly). For what it’s worth, compact_vector hits ~25% memory overhead at around 200 elements (for the 64 bit version), and by 1000 elements we’re already down to around 10% (these figures get better for larger elements since the index block part of the overhead depends on element count and pointer size, not element size).
Anyway, I’ll stop talking now. Hope this is useful to someone!
UPDATE: And here’s a view of the actual overhead zoomed in to the first 4000 insertions. This shows you better how memory use isn’t just a difference in “spikiness” (allocation rate), the compact_vector genuinely tends to much lower overhead asymptotically compared to std::vector. The latter’s overhead averages out at 25% in the graph below (as expected), whereas the compact_vector quickly converges on single-digit percent overheads.